相关文章
Linux PAGE_ALIGN 宏定义的理解
前言
最近再阅读 Linux ion（一种内存分配管理）时，遇到了 PAGE_ALIGN 宏，这个宏到底是怎么工作的？ 【页对齐】时什么意思？ 页大小就是 4096 吗？
追踪 PAGE_ALIGN 通过一步一步的追踪࿰…
编程日记
2024/12/8 21:21:02
c: Queue Calling in Ubuntu
/*** file TakeNumber.h* author your name (geovindu)* brief * version 0.1* date 2023-10-20* * copyright Copyright (c) 2023 站在巨人的肩膀上 Standing on the Shoulders of Giants* */#ifndef TAKENUMBER_H
#define TAKENUMBER_H#include <stdio.h>
#include <…
编程日记
2024/12/16 1:22:38
Git（一）Windows下安装及使用Git Bash
目录 一、简介1.1 什么是Git？1.2 Git 的主要特点1.3 什么是 Git Bash？ 二、下载三、安装3.1 同意协议3.2 选择安装位置3.3 其他配置（【Next】 即可）3.4 安装完毕3.5 打开 Git Bash 官网地址： https://www.git-scm.com/…
编程日记
2024/12/21 22:36:41
Jupyter使用技巧-环境篇
不同于其他IDE，有时会出现找不到文件路径，通常是因为当前工作目录（working directory）不同所导致的。Jupyter Notebook 会在启动时选择一个初始的工作目录，而这个目录可能与你运行 .py 文件时所在的目录不同。
import…
编程日记
2024/12/19 18:51:35
AM@麦克劳林公式逼近以及误差分析
abstract
麦克劳林公式及其近似表示的应用误差估计和分析
Lagrange型泰勒公式的估计误差
由Lagrange型余项泰勒公式可知,多项式 p n ( x ) p_n(x) pn(x)近似表达函数 f ( x ) f(x) f(x)时,其误差为 ∣ R n ( x ) ∣ |R_{n}(x)| ∣Rn(x)∣ R n ( x ) R_{n}(x) Rn(x) f …
编程日记
2024/12/21 17:53:04
C语言用awtk开发界面访问http接口
AWTK全称为Toolkit AnyWhere，是ZLG倾心打造的一套基于C语言开发的GUI框架。旨在为用户提供一个功能强大、高效可靠、简单易用、可轻松做出炫酷效果的GUI引擎，并支持跨平台同步开发，一次编程，终生使用。 1. 初识AWTK | AWStudio社区…
编程日记
2024/12/21 9:46:23
聊聊分布式架构10——Zookeeper入门详解
目录
01ZooKeeper的ZAB协议
ZAB协议概念
ZAB协议基本模式
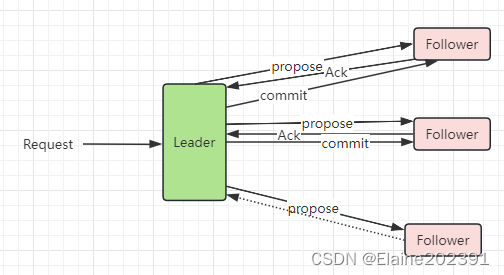
消息广播
崩溃恢复
选举出新的Leader服务器
数据同步
02Zookeeper的核心
ZooKeeper 的核心特点
ZooKeeper 的核心组件
选举算法概述
服务器启动时的Leader选举
服务器运行期间的Leader选举
03ZooKeeper的…
编程日记
2024/12/22 22:37:30
Cocos的基本操作，实用操作
1.场景加载 cc.director.loadScene(场景名称);//场景跳转 cc.director.preloadScene(场景名称);//预加载场景
cc.director.getScene();//获取当前场景
2.获取节点 var node cc.find("Canvas/bg");//通过访问路径来获取节点
var a this.node.getChildByName(name…
编程日记
2024/12/20 23:27:05
