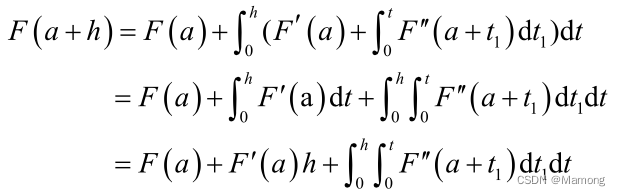相关文章
第一章《补基础:不怕学不懂微积分》笔记
微积分包含众多知识点,例如极限概念、求导公式、乘积法则、链式法则、隐函数求导、 积分中值定理、泰勒公式等。其中,研究导数、微分及其应用的部分一般称为微分学,研究不定积分、定积分及其应用的部分一般称为积分学。微分学和积分学统称为微…
编程日记
2025/3/10 20:35:06
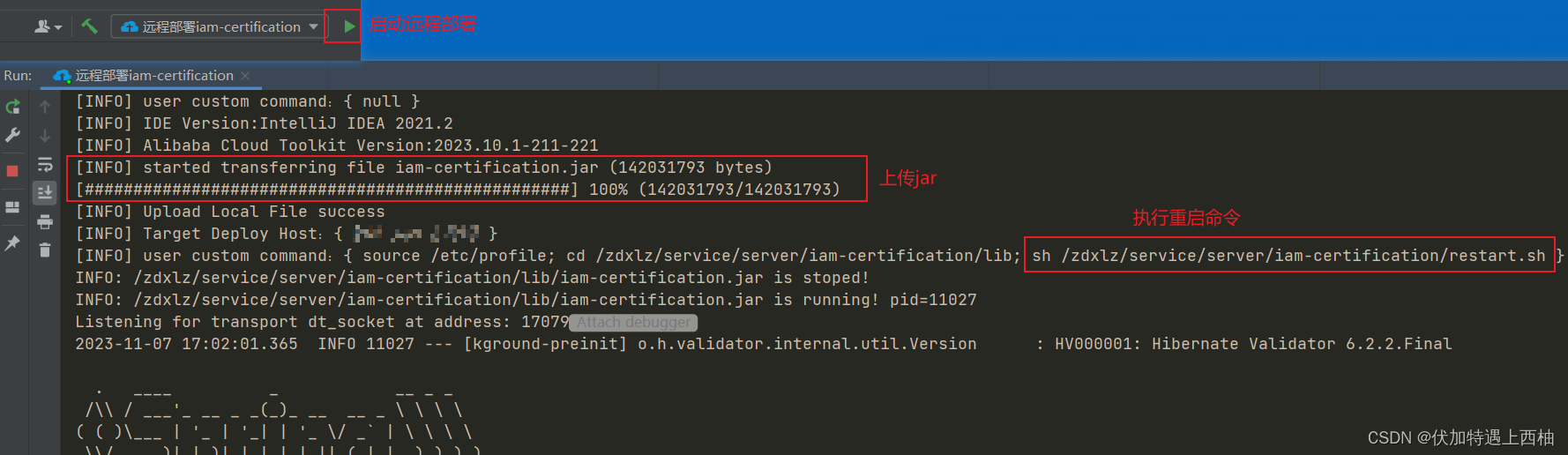
ideal一键部署SpringBoot项目jar包到服务器
一 简介
我们在开发环境部署项目一般通过ideal将项目打包成jar包,然后连接linux服务器,将jar手动上传到服务中,重启服务。 概括的说流程是这样的: 本地打包->上传到服务器->kill掉以前的服务->重新启动jar包服务
每次总是循环这一…
编程日记
2025/3/9 13:15:30
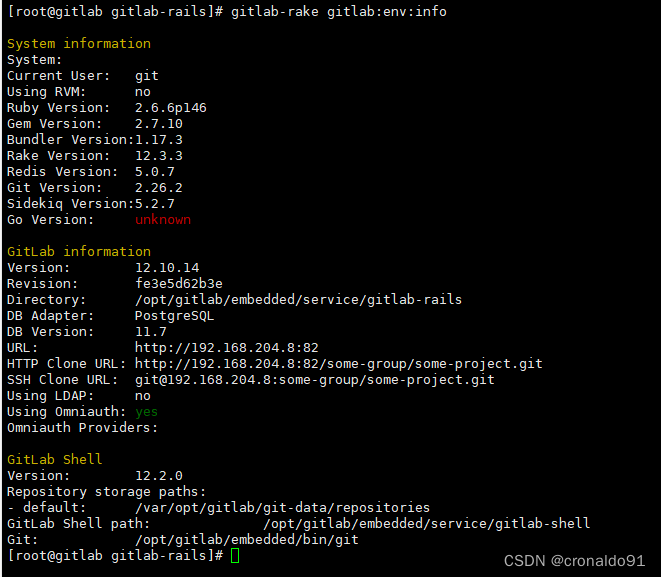
持续集成交付CICD:安装Gitlab Runner(从节点)
目录
一、实验
1.选择Gitlab Runner版本
2.安装Gitlab Runner(第一种方式:交互式安装)
3.安装Gitlab Runner(第二种方式:非交互式安装)
二、问题
1.如何查看Gitlab版本 一、实验
1.选择Gitlab Runne…
编程日记
2025/3/8 1:36:47
C++11 shared_ptr类型智能指针学习
智能指针和普通指针的用法类似,但是智能指针可以在适当时机自动释放分配的内存。
C++11有三种类型的智能指针,shared_ptr、unique_ptr 以及 weak_ptr; 先学习shared_ptr类型;
shared_ptr<T> 的定义位于<memory>头文件,并位于 std 命名空间中; T 表示指针指…
编程日记
2025/3/10 1:52:08
如何修改CentOS登录时默认目录
查了一下,有说改/etc/passwd文件的,有说改.bashrc文件的,也有说改.bash_profile,修改的方法都不一样。
我要改的是root登录时的目录,最后修改了/root/.bash_profile文件,只要加一行cd 路径就可以。 这个文…
编程日记
2025/3/10 14:25:01
Docker的安装以及使用
每次安装Docker都会报一堆错,痛定思痛干脆自己总结一篇!!! Docker的安装
卸载系统自带的旧版本
sudo apt-get remove docker docker-engine docker.io containerd runc
获取软件最新源
sudo apt-get update
安装apt依赖包
s…
编程日记
2025/3/11 6:40:49