相关文章
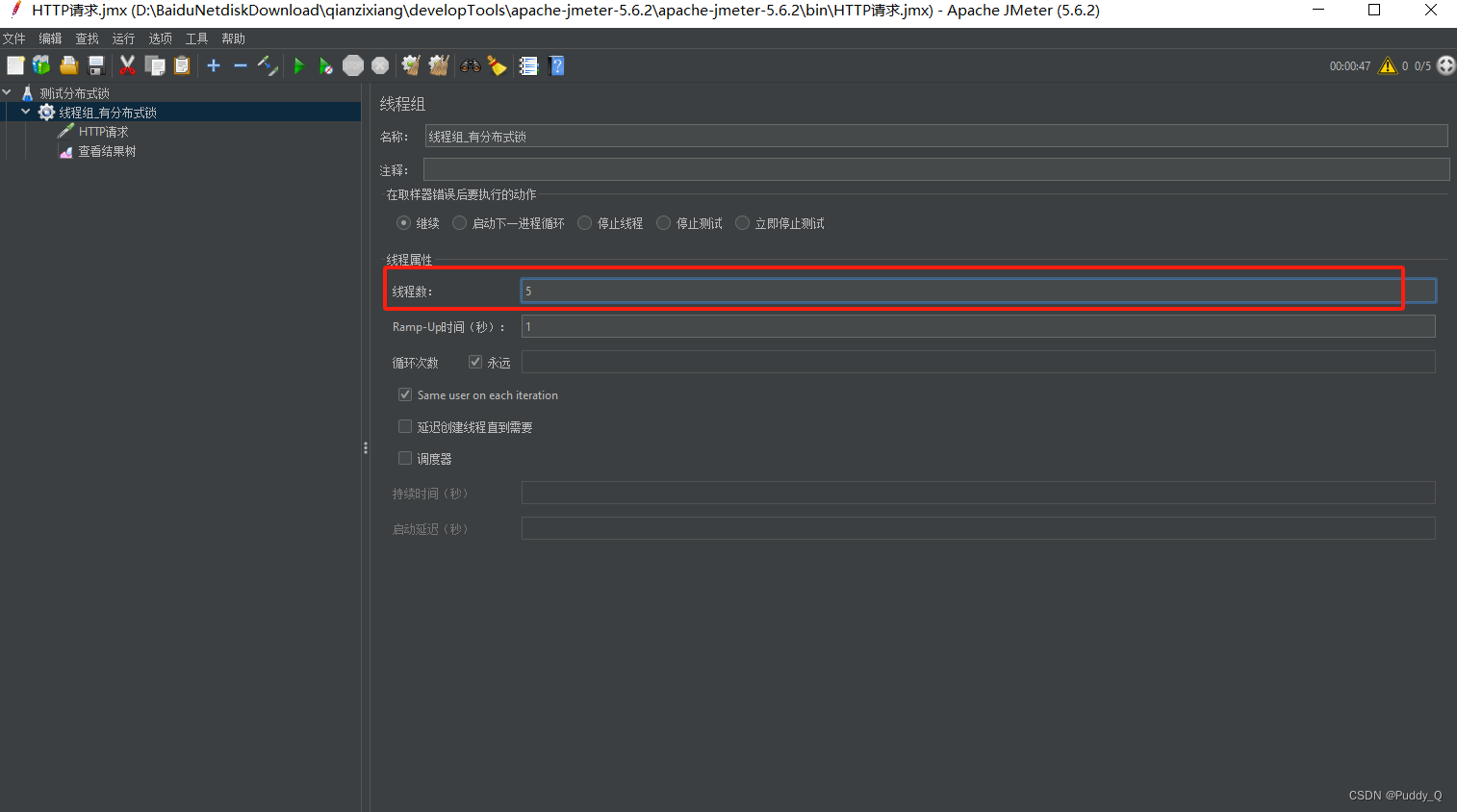
如何实现Redisson分布式锁
首先,不要将分布式锁想的太复杂,如果我们只是平时业务中去使用,其实不算难,但是很多人写的文章不能让人快速上手,接下来,一起看下Redisson分布式锁的快速实现 Redisson 是一个在 Redis 的基础上实现的 Java…
编程日记
2025/3/27 20:02:47
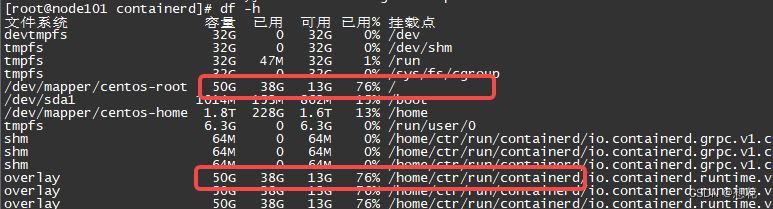
报错资源不足,k8s使用containerd运行容器修改挂载点根目录换成/home
运行k8s一段时间发现存储不足报错 发现这里用的是根路径的挂载,修改一下
编程日记
2025/3/30 9:07:52
黑马程序员微服务Docker实用篇
Docker实用篇
0.学习目标
1.初识Docker
1.1.什么是Docker
微服务虽然具备各种各样的优势,但服务的拆分通用给部署带来了很大的麻烦。
分布式系统中,依赖的组件非常多,不同组件之间部署时往往会产生一些冲突。在数百上千台服务中重复部署…
编程日记
2025/3/28 14:22:55
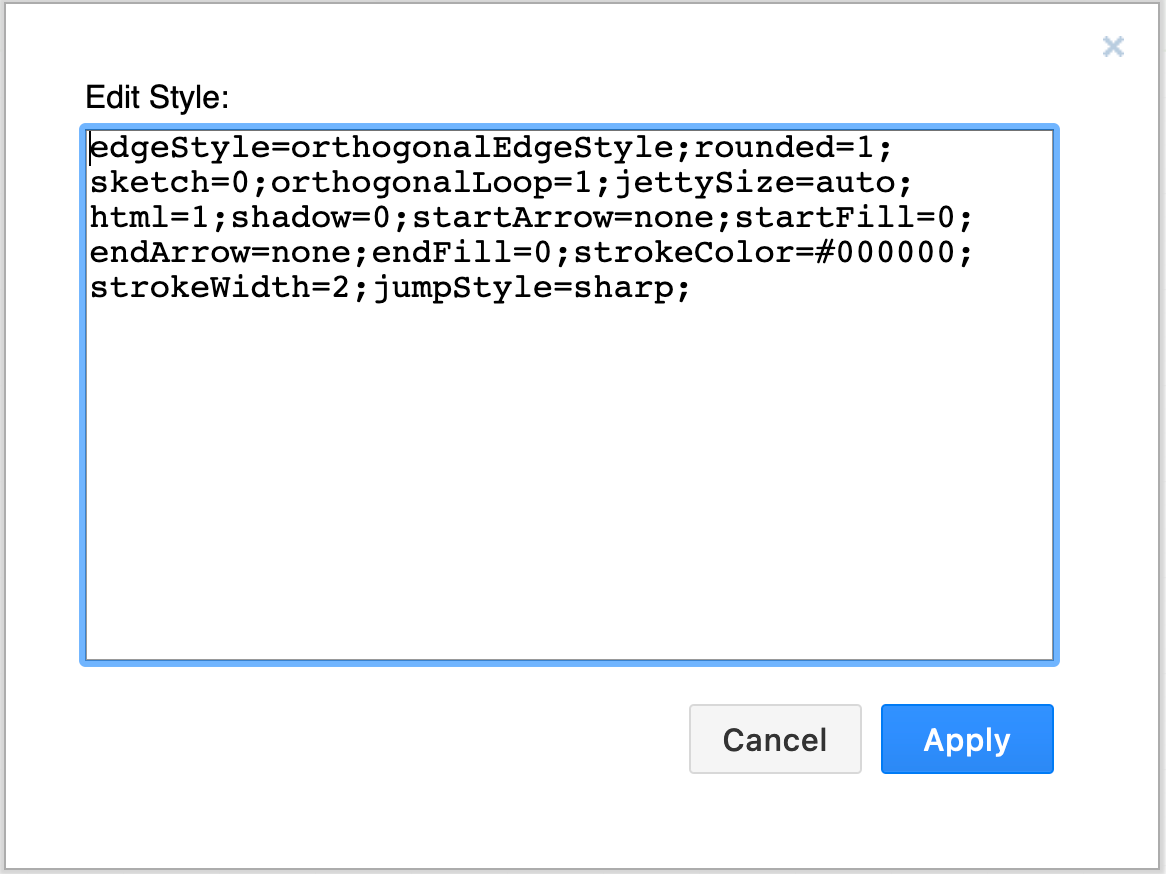
drawio连接线的样式设置
drawio是一款强大的图表绘制软件,支持在线云端版本以及windows, macOS, linux安装版。 如果想在线直接使用,则直接输入网址draw.io或者使用drawon(桌案), drawon.cn内部完整的集成了drawio的所有功能,并实现了云端存储,以及在线共…
编程日记
2025/4/2 13:52:04
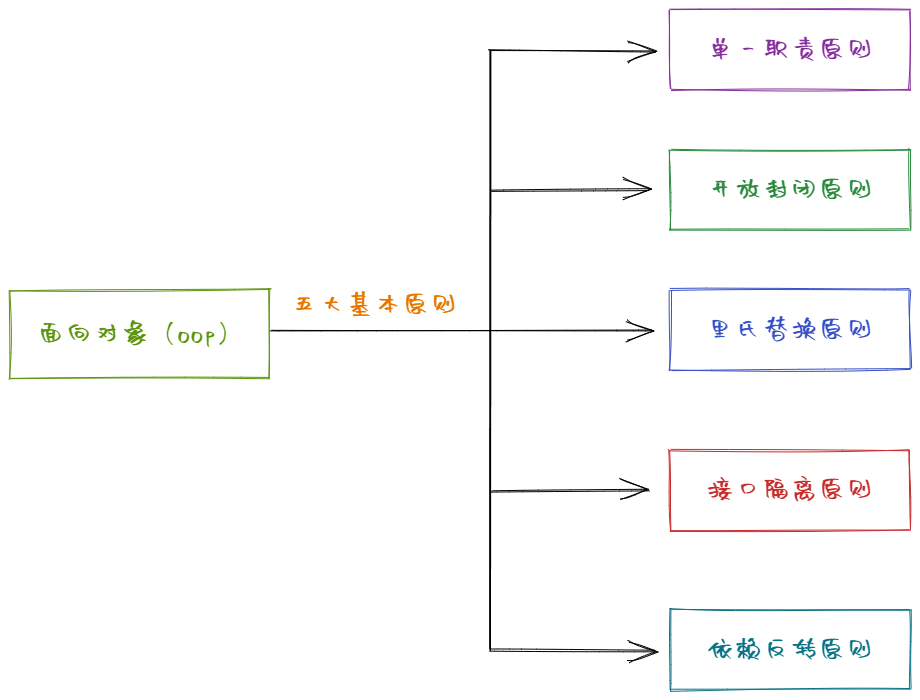
八股文-面向对象的理解
近年来,IT行业的环境相较以往显得有些严峻,因此一直以来,我都怀有一个愿望,希望能够创建一个分享面试经验的网站。由于个人有些懒惰,也较为喜欢玩乐,导致计划迟迟未能实现。然而,随着年底的临近…
编程日记
2025/3/29 21:09:46
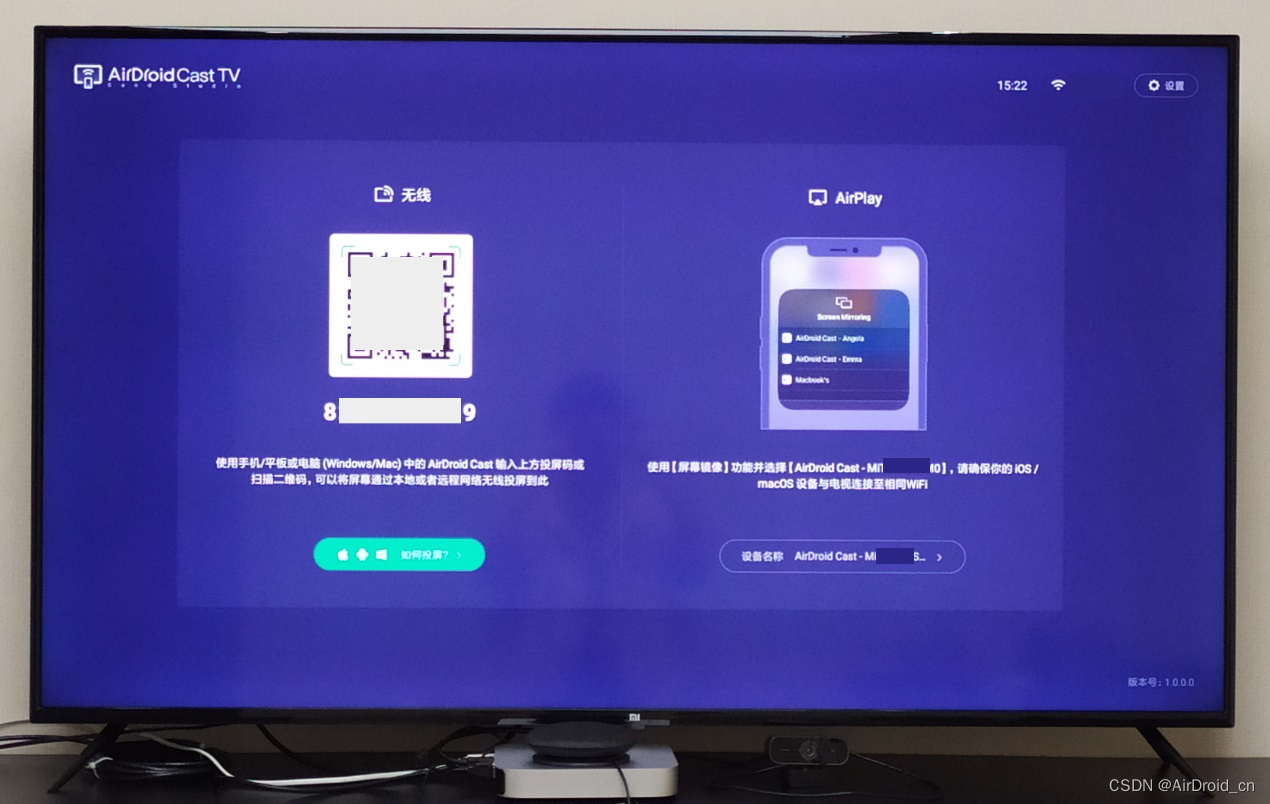
Linux电脑投屏到电视的简洁操作
Linux电脑投屏到安卓电视有多种好处。 首先,通过将Linux电脑与安卓电视连接,用户可以轻松地将电脑屏传输到电视上,从而获得更加舒适和清晰的视觉体验。 其次,投屏功能可以帮助用户在电视上展示电脑中的图片、视频和其他多媒体文件…
编程日记
2025/3/31 18:41:34
线性代数本质系列(一)向量,线性组合,线性相关,矩阵
本系列文章将从下面不同角度解析线性代数的本质,本文是本系列第一篇
向量究竟是什么? 向量的线性组合,基与线性相关 矩阵与线性相关 矩阵乘法与线性变换 三维空间中的线性变换 行列式 逆矩阵,列空间,秩与零空间 克莱姆…
编程日记
2025/3/29 9:09:25
27 微服务配置拉取
1)引入nacos-config依赖
首先,在user-service服务中,引入nacos-config的客户端依赖:
<!--nacos配置管理依赖-->
<dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-sta…
编程日记
2025/3/27 16:13:34