相关文章
MATLAB程序设计课后作业三、四
1、课程中学习到kmeans聚类函数,查询kmeans算法的基本原理,还有什么其他类型的聚类算法?
层次聚类算法,它不需要预先指定簇的个数,而是通过构建数据点的层次结构来进行聚类,可以得到不同层次的聚类结果。一…
编程日记
2024/12/23 17:59:55
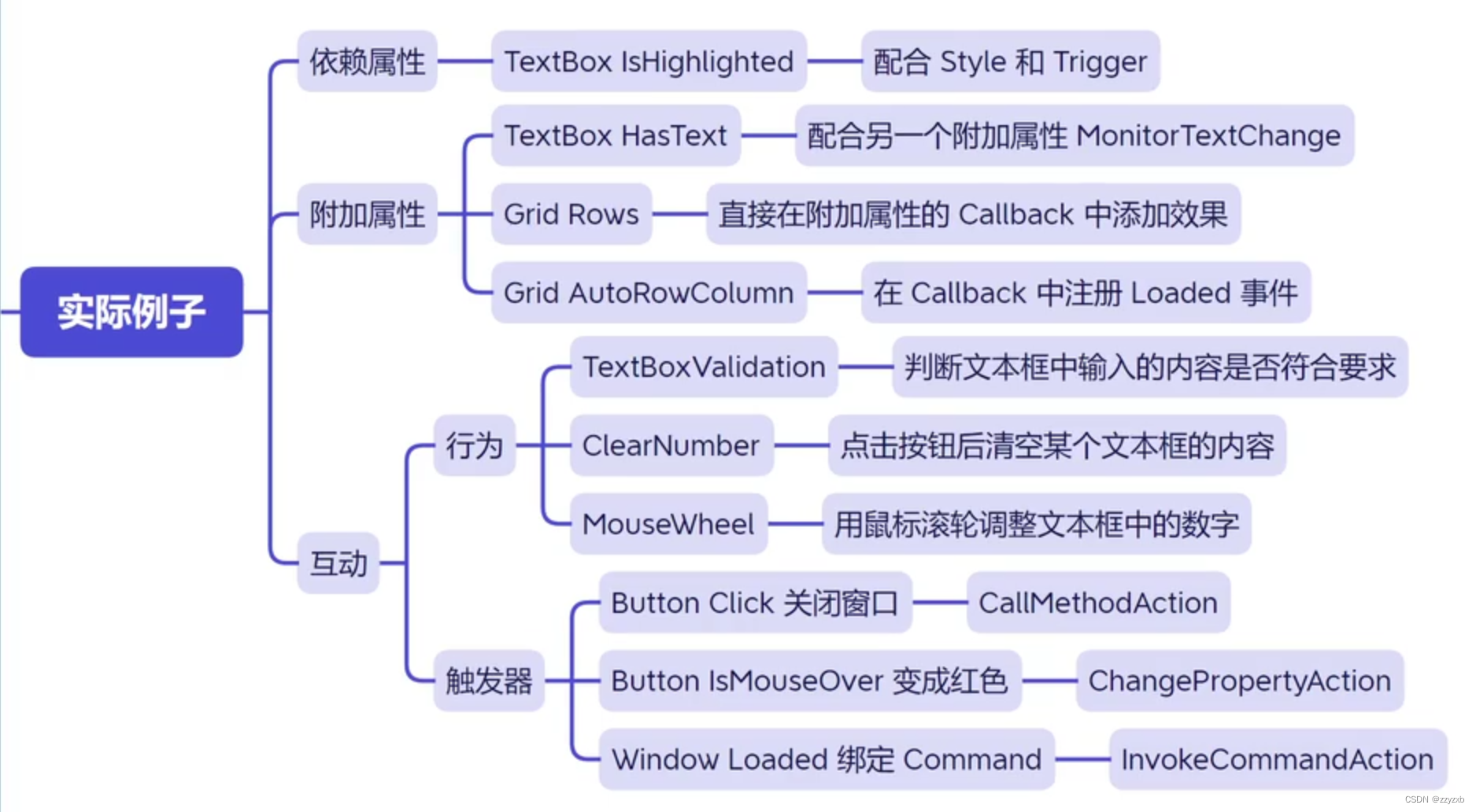
WPF中行为与触发器的概念及用法
完全来源于十月的寒流,感谢大佬讲解
一、行为 (Behaviors) behaviors的简单测试
<Window x:Class"Test_05.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winf…
编程日记
2024/12/23 18:20:29
MySQL 的执行原理(一)
5.1 单表访问之索引合并
我们前边说过 MySQL 在一般情况下执行一个查询时最多只会用到单个二级 索引,但存在有特殊情况,在这些特殊情况下也可能在一个查询中使用到多个二 级索引,MySQL 中这种使用到多个索引来完成一次查询的执行方法称之为&…
编程日记
2024/12/21 3:40:20
用人话讲解深度学习中CUDA,cudatookit,cudnn和pytorch的关系
参考链接
本人学习使用,侵权删谢谢。用人话讲解深度学习中CUDA,cudatookit,cudnn和pytorch的关系
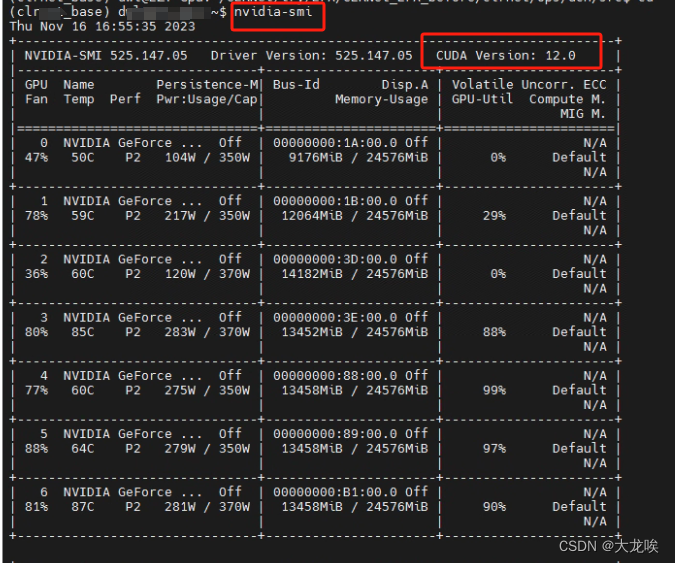
CUDA
CUDA是显卡厂商NVIDIA推出的运算平台。 CUDA™是一种由NVIDIA推出的通用并行计算架构,是一种并行计算平台和编程模型&…
编程日记
2024/12/21 18:31:14
Linux | C语言中volatile关键字的理解
目录
前言
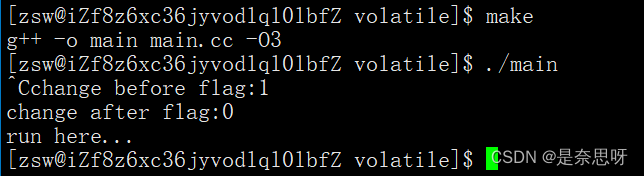
一、代码引入
二、现象解释
三、具体引用 前言 本章主要讲解介绍volatile关键的作用与使用场合;深刻理解volatile关键字;本文你需要有信号相关的基础知识; Linux | 信号-CSDN博客 一、代码引入 首先,我们来查看下面…
编程日记
2024/12/20 13:15:43
实测文心一言4.0,真的比GPT-4毫不逊色吗?
10月17日,李彦宏在百度世界2023上表示。当天,李彦宏以《手把手教你做AI原生应用》为主题发表演讲,发布文心大模型4.0版本。
今天,咱们就开门见山啊。这一回要测一测,昨天才发布的文心一言大模型 4.0。
之所以要测它&…
编程日记
2024/12/23 4:38:43