相关文章
基于Kafka2.1解读Consumer原理
文章目录 概要整体架构流程技术名词解释技术细节coordinatorfetcherclientconsumer#poll的主要流程 全局总览小结 概要
继上一篇讲Producer原理的文章过去已经一个多月了,今天来讲讲Consumer的原理。 其实源码早就读了部分了,但是最近工作比较忙&#x…
编程日记
2025/1/22 7:28:16
React Native 全栈开发实战班 - 本地存储实现
在移动应用中,本地存储 是实现数据持久化的重要手段。React Native 提供了多种本地存储方案,包括异步存储(AsyncStorage)、SQLite 数据库以及其他第三方库。本章节将介绍如何使用 AsyncStorage 进行简单的键值对存储,以…
编程日记
2025/1/23 22:14:36
(长期更新)《零基础入门 ArcGIS(ArcMap) 》实验一(下)----空间数据的编辑与处理(超超超详细!!!)
续上篇博客(长期更新)《零基础入门 ArcGIS(ArcMap) 》实验一(上)----空间数据的编辑与处理(超超超详细!!!)-CSDN博客 继续更新 本篇博客内容为道路拓扑检查与修正&#x…
编程日记
2025/1/22 23:46:35
大数据新视界 -- 大数据大厂之 Impala 性能飞跃:分区修剪优化的应用案例(下)(22 / 30)
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…
编程日记
2025/1/23 3:10:59
若点集A=B则A必能恒等变换地变为B=A这一几何常识推翻直线(平面)公理
黄小宁
关键词:“更无理”复数
复平面z各点z的对应点z1的全体是z1面。z面平移变为z1面就使x轴⊂z面沿本身平移变为ux1轴。R可几何化为R轴,R轴可沿本身平移变为R′轴,R′轴可沿本身平移变为R″轴,...。直线公理和平面公理使几百年…
编程日记
2025/1/23 6:19:28
【数据库】mysql数据库迁移前应如何备份数据?
MySQL 数据库的备份是确保数据安全的重要措施之一。在进行数据库迁移之前,备份现有数据可以防止数据丢失或损坏。以下是一套详细的 MySQL 数据库备份步骤,适用于大多数情况。请注意,具体的命令和工具可能因 MySQL 版本的不同而有所差异。整个…
编程日记
2025/1/22 14:49:40
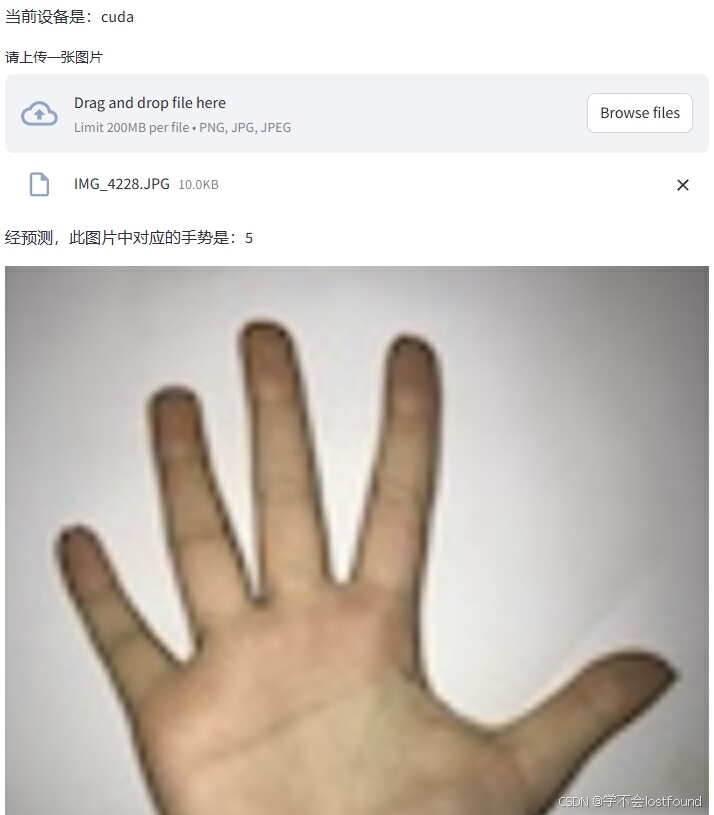
三、计算机视觉_03LeNet5及手势识别案例
1 LeNet-5基本介绍 LeNet-5是一种经典的卷积神经网络(CNN)架构,由Yann LeCun在1998年提出,用于手写数字识别,LeNet-5是卷积神经网络的开创性工作之一,它引入了卷积层、池化层和全连接层的组合,为…
编程日记
2025/1/21 23:06:00
【项目开发】URL中井号(#)的技术细节
未经许可,不得转载。 文章目录 前言一、# 的基本含义二、# 不参与 HTTP 请求三、# 后的字符处理机制四、# 的变化不会触发网页重新加载五、# 的变化会记录在浏览器历史中六、通过 window.location.hash 操作七、onhashchange 事件八、Google 对 # 的处理机制前言
2023 年 9 月…
编程日记
2025/1/23 3:29:28